On the nonuniqueness of the
Navier–Stokes initial value problem

Julien Guillod
September 18, 2017
Mathematical Analysis of Incompressible Fluid Flows
Brighton
Joint work with
Vladimír Šverák

1. Introduction
Navier–Stokes equations
$$\begin{cases}
\partial_{t}\bu+\bu\bcdot\bnabla\bu=\Delta\bu-\bnabla p\\
\bnabla\bcdot\bu=0\\
\bu(0)=\bu_{0}
\end{cases}
\quad \text{in} \quad \mathbb{R}^3\tag{NS}$$
Main question
Well-posedness of the Cauchy problem (existence, uniqueness, regularity)
Main two methods
- energy method (a priori bounds)
- perturbation method (Banach fixed point)
Energy method
- A priori bound on the energy:$$\left\Vert \bu(t)\right\Vert _{L^{2}(\mathbb{R}^{3})}^{2}+2\int_{0}^{t}\left\Vert \bnabla\bu(\tau)\right\Vert _{L^{2}(\mathbb{R}^{3})}^{2}\rd\tau\leq\left\Vert \bu_0\right\Vert _{L^{2}(\mathbb{R}^{3})}^{2}$$
- Leray–Hopf solution on $(0,T)$: $$\bu \in L^{\infty}(0,T;L^{2}(\mathbb{R}^{3}))\cap L^{2}(0,T;\dot{H}^{1}(\mathbb{R}^{3}))$$ satisfying (NS) in the sense of distribution and the energy inequality.
Theorem (Leray, 1934)
For any $\bu_0\in L^2(\mathbb{R}^3)$, existence of a global Leray–Hopf solution ($T=\infty$). The regularity and uniqueness of these weak solutions are open.
Perturbation method
- Inversion of the linearity on the nonlinearity: $$\bu(t)=\e^{\Delta t}\bu_0+\int_{0}^{t}\e^{\Delta(t-\tau)}\mathbb{P}\bigl(\bu(\tau)\bcdot\bnabla\bu(\tau)\bigr)\,\rd\tau$$
- Mild solution in $X_T$: $$\bu \in X_T \quad\text{for some}\quad T>0$$ satisfying the above equation for all $t\in [0,T)$.
Question
In which function spaces a fixed point argument can be made for short time?
Criticality
- Criticality:
- subcritical spaces: linearity dominant (easy)
- critical spaces: linearity and nonlinearity balanced
- supercritical spaces: nonlinearity dominant (hard)
- Scaling symmetry: $$\begin{aligned}\bu_{\lambda}(t,\bx) & =\lambda\bu(\lambda^{2}t,\lambda\bx)\\ p_{\lambda}(t,\bx) & =\lambda^{2}p(\lambda^{2}t,\lambda\bx)\\ \bu_{0\lambda}(\bx) & =\lambda\bu_{0}(\lambda\bx)\end{aligned}$$
- Critical space:
Banach space $X$ of functions $(0,\infty)\times\mathbb{R}^3\to\mathbb{R}^3$ such that $$\Vert\bu_\lambda\Vert_X = \Vert\bu\Vert_X$$ - Critical spaces are a priori the largest ones where a fixed point argument is expected to close.
Critical spaces $L^{p}(0,T;L^{q}(\mathbb{R}^{3}))$
Theorem (Kato, 1984)
For $q\geq3$ and $\bu_0\in L^q(\mathbb{R}^3)$, existence of a local mild solution $\bu\in L^\infty(0,T;L^q(\mathbb{R}^3))$, which is global if $\bu_0$ is small enough.
Theorem (Prodi, 1959; Serrin, 1963; Ladyzhenskaya, 1967;
Escauriaza et al., 2003)
Escauriaza et al., 2003)
If $\bu\in L^{p}(0,T;L^{q}(\mathbb{R}^{3}))$ with $\frac{2}{p}+\frac{3}{q}\leq1$, then $\bu$ is smooth and unique on $(0,T)$.
Critical spaces $L^\infty(0,T;X)$
- If $X$ is a Banach spaces of functions $\mathbb{R}^3\to\mathbb{R}^3$ such that $$\Vert\bu_{0\lambda}\Vert_X = \Vert\bu_0\Vert_X$$ then $L^\infty(0,T;X)$ is a critical space.
- Two families: $$\begin{align*} X & = L^{3}(\mathbb{R}^{3}),\; \dot{H}^{1/2}(\mathbb{R}^{3}),\dots & \text{with}\quad\frac{1}{|\bx|} & \notin X\\ \overline{X} & =L^{3,\infty}(\mathbb{R}^{3}),\; BMO^{-1},\dots & \text{with}\quad\frac{1}{|\bx|} & \in \overline{X} \end{align*}$$
- Hidden smallness condition in $X$ not in $\overline{X}$: $$\bu_{0\lambda}\big|_{B_R}\to0 \quad\text{as}\quad \lambda\to0 \quad\text{for any}\quad \bu_0\in X$$
Critical spaces $L^\infty(0,T;\overline{X})$
Theorem (Koch & Tataru, 2001)
For $\bu_0\in BMO^{-1}(\mathbb{R}^3)$ with $\bu_0\big|_{B_R}$ small enough in $BMO^{-1}(B_R)$ for some $R>0$, existence of a unique solution with $T=R^2$.
Intuition
- For $\bu_0\in X$ : short time with large data
For $\bu_0\in X$ : large time with small data - For $\bu_0\in \overline{X}$ : only for small data
For $\bu_0\in \overline{X}$ : (supercritical regime from $t=0$)
Question on the nonperturbative regime
What is happening for large data in the spaces $\overline{X}$?
Scale-invariant solutions
- Scale-invariant initial data: $$u_{0\lambda}=u_0 \quad\textit{i.e.}\quad u_0(\bx)=\frac{\varphi(\hat{\bx})}{|\bx|}$$
- Scale-invariant solutions: $$u_{\lambda}=u \quad\textit{i.e.}\quad u(t,\bx)=\frac{1}{t^{1/2}}U\Bigl(\frac{\bx}{t^{1/2}}\Bigr)$$
- Ansatz into (NS): $$\begin{cases} \Delta\bU+\frac{\bx}{2}\bcdot\bnabla\bU+\frac{1}{2}\bU-\bU\bcdot\bnabla\bU-\bnabla P=\bzero\\ \bnabla\bcdot\bU=0\\ \bU(\bx)=\bu_{0}(\bx)+o(\left|\bx\right|^{-1})\quad\text{as}\quad\left|\bx\right|\to\infty \end{cases}\tag{NS-self}$$
- Short form: $$\text{(NS-self)} \quad\Longleftrightarrow\quad F(\bU)=\bzero$$
Existence of scale-invariant solutions
Theorem (Jia & Šverák, 2013)
For $\bu_0\in C^\infty(\mathbb{R}^3\setminus\{\bzero\})$ scale-invariant, there exists al least one scale-invariant solution $\bu\in C^\infty((0,\infty)\times\mathbb{R}^3)$. Moreover the profile $\bU\in C^\infty(\mathbb{R}^3)$ satisfies $$\bigl|\bU(\bx)-\e^{\Delta}\bu_{0}(\bx)\bigr|\leq\frac{C(\bu_{0})}{\left(1+\left|\bx\right|\right)^{3}}$$
Intuition for the proof
Since (NS-self) is elliptic, use Leray–Schauder as for proving the existence of steady solutions to the Navier–Stokes equations. Therefore, the solution is a priori unique only for small $\bu_0$.
2. Results
Aim and Strategy
Aim
Find a self-similar $\bu_0$ such that the Navier–Stokes equations admit at least two different self-similar solutions.
Strategy
- Work within the class of axisymmetric solutions (with swirl)
- Choose a self-similar initial data with pure swirl: $$\bu_0(r,z) = \sigma(r^{2}+z^{2})^{-1/2}f(z/r)\,\be_{\theta}$$
- Find a numerical solution $\bU_\sigma$ by continuation in $\sigma\geq0$
- Numerically compute the spectrum of $DF(\bU_\sigma)$ for each $\sigma\geq0$
- Resolve the solutions possibly bifurcating form $\bU_\sigma$
Numerical solution $\bU_\sigma$
Spectrum of $DF(\bU_\sigma)$
Bifurcation
$\sigma=\,$0
Bifurcated solution
Streamlines
Nonuniqueness in $L^\infty(0,T,L^{3,\infty}(\mathbb{R}^3))$
Spectral numerical results
On the range $\sigma\in[0,500]$, there exists a unique axisymmetric self-similar solution $\bU_\sigma$ that is symmetric with respect to the plane $z=0$. The spectrum of the linearization $DF(\bU_\sigma)$ has the form $$\sigma(DF(\bU_\sigma))\subset\bigl\{\lambda\in\mathbb{C}\,:\:\mathrm{Re}\,\lambda>\delta\bigr\}\cup\bigl\{\lambda_{\sigma}\bigr\}\,,\tag{$*$}$$
for some $\delta>0$ and there exists $\sigma_{0}\approx292$ such that $\lambda_{\sigma}>0$ for $\sigma<\sigma_{0}$, $\lambda_{\sigma}=0$ for $\sigma=\sigma_{0}$, and $\lambda_{\sigma}<0$ for $\sigma>\sigma_{0}$.
Nonuniqueness numerical results
There exists two different smooth solutions in $L^\infty(0,T;L^{3,\infty}(\mathbb{R}^3))$ with the same scale-invariant initial data $\bu_0\in L^{3,\infty}(\mathbb{R}^3)$.
Nonuniqueness of Leray–Hopf solutions
Theorem (adapted from Jia & Šverák, 2015)
Under the spectral assumption ($*$), there exists two different smooth Leray–Hopf solutions with the same compactly supported initial data $\bu_{0}\in C^{\infty}(\mathbb{R}^{3}\setminus\{\bzero\})$
with $\bu_{0}(\bx)=O(\left|\bx\right|^{-1})$
near the origin. Moreover these two solutions belongs to $L^{p}(0,T;L^{q}(\mathbb{R}^{3}))$
for any $$\frac{2}{p}+\frac{3}{q}>1\qquad\text{and}\qquad q\geq2\,.$$
Corollary
The known perturbation results are essentially optimal.
Nonuniqueness in supercritical region
3. Speculations
Philosophy
Hypothesis
Maybe what is not forbidden is allowed?
Examples on positive side
- Double exponential growth for 2D Euler (Kiselev & Šverák, 2014)
- Onsager conjecture for 3D Euler (Isett, 2016)
Examples on negative side
- Global well-posedness for Burgers (Kiselev & Ladyzhenskaya, 1957)
- Global well-posedness for Template matching (Plecháč & Šverák, 2003)
Plausible scenario
Finite-time blow-up by generalized
scale-invariant solutions?
Theorem (Tsai, 1998)
There is no reasonable scale-invariant solutions blowing-up in finite time.
Main idea
Combine the rotational and scaling symmetries:
$$u(t,\bx) = \e^{\lambda}\e^{-\lambda\bL}\bu(\e^{2\lambda}t,\e^{\lambda}\e^{\lambda\bL}\bx)$$
where $\bL\in \mathfrak{so}(3)$ i.e.
$$u(t,\bx) = \frac{\e^{\frac{1}{2}\log(-t)\bL} }{(-t)^{1/2}} \bU\Bigl(\frac{\e^{-\frac{1}{2}\log(-t)\bL}\bx}{(-t)^{1/2}}\Bigr)$$
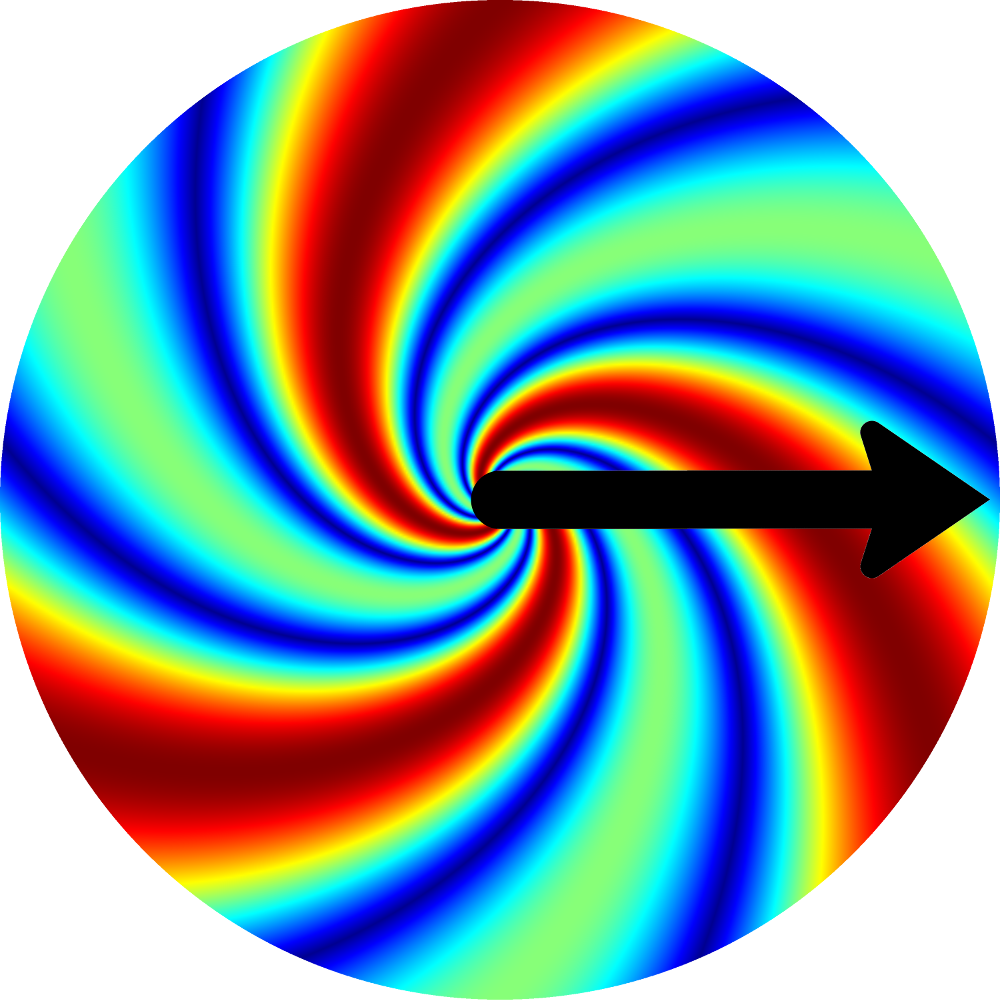

steady solution in $\mathbb{R}^2\setminus\{\bzero\}$
(Guillod & Wittwer, 2015)
(Guillod & Wittwer, 2015)