Generalized scale-invariant solutions to the two-dimensional stationary Navier–Stokes equations

Abstract

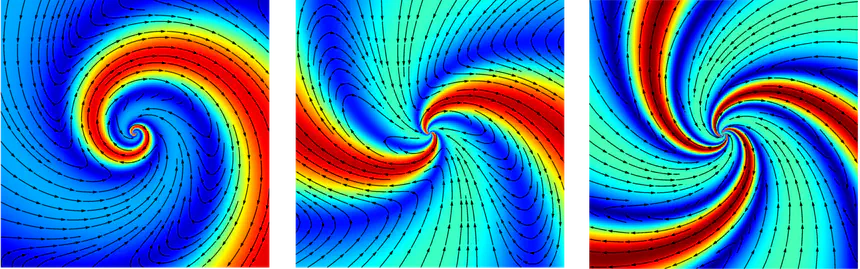
New explicit solutions to the incompressible Navier–Stokes equations in $\mathbb{R}^2 \setminus \{0\}$ are determined, which generalize the scale-invariant solutions found by Hamel. These new solutions are invariant under a particular combination of the scaling and rotational symmetries. They are the only solutions invariant under this new symmetry in the same way as the Hamel solutions are the only scale-invariant solutions. While the Hamel solutions are parameterized by a discrete parameter $n$, the flux $\Phi$, and an angle $\theta_0$, the new solutions generalize the Hamel solutions by introducing an additional parameter $\kappa$ which produces a rotation. The new solutions decay like $|\boldsymbol{x}|^{-1}$ as the Hamel solutions and exhibit spiral behavior. The new variety of asymptotes induced by the existence of these solutions further emphasizes the difficulties faced when trying to establish the asymptotic behavior of the Navier–Stokes equations in a two-dimensional exterior domain or in the whole plane.

Movies

Scale-invariant solutions up to a rotation

Animation 1: A scale-invariant solution $\boldsymbol{u}$ up to a rotation characterized by $\kappa$ is a solution which remains invariant by a combination of a scaling and of a rotation, i.e. such that $\boldsymbol{u}(\boldsymbol{x}) = e^\lambda \mathbf{R} _{\kappa\lambda} \boldsymbol{u}(e^\lambda \mathbf{R} _{-\kappa\lambda}\boldsymbol{x})$ for all $\lambda$, where $\mathbf{R} _{\theta}$ is the matrix of rotation of angle $\theta$.

Velocity field of the generalized Hamel solutions for κ = 0.0

n = 2

n = 3

n = 4

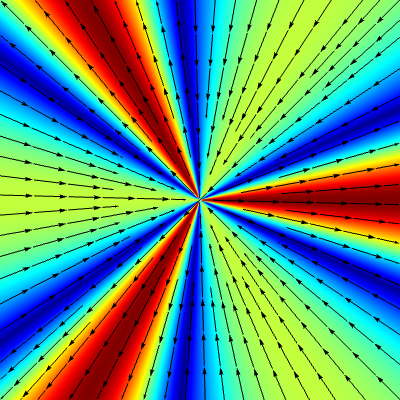
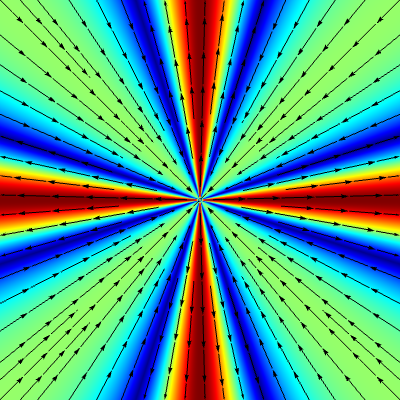
Animation 2: At fixed values of $\kappa$, the scale-invariant solutions of the Navier–Stokes equations up to a rotation are discrete. At $\kappa = 0$, they correspond to the Hamel solutions which are scale-invariant and as $\kappa$ increases, they have a spiral behavior.