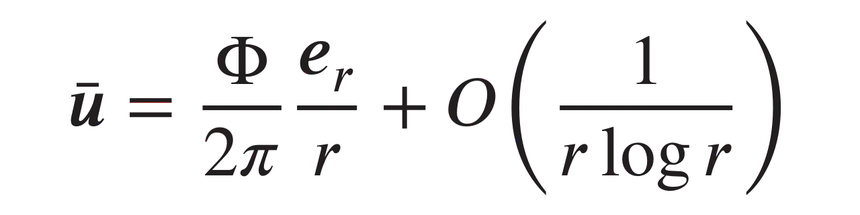
On the asymptotic stability of steady flows with nonzero flux in two-dimensional exterior domains

Abstract

The Navier–Stokes equations in a two-dimensional exterior domain are considered. The asymptotic stability of stationary solutions satisfying a general hypothesis is proven under any $L^2$-perturbation. In particular the general hypothesis is valid if the steady solution is the sum of the critically decaying flux carrier with flux $|\Phi|<2\pi$ and a small subcritically decaying term. Under the central symmetry assumption, the general hypothesis is also proven for any critically decaying steady solutions under a suitable smallness condition.