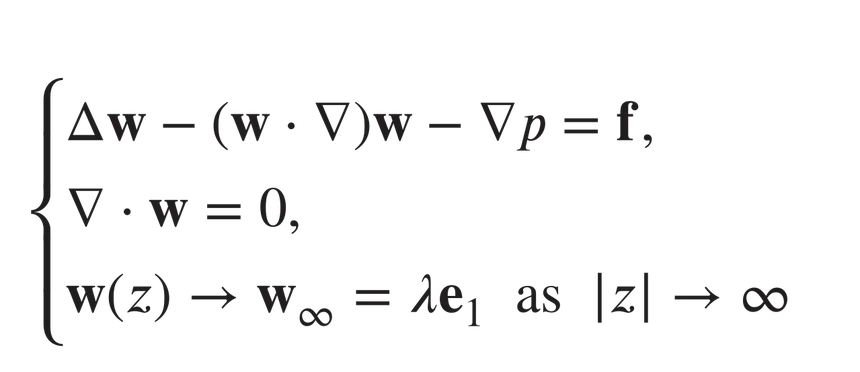Existence and uniqueness for plane stationary Navier–Stokes flows with compactly supported force

Abstract

We study the stationary Navier–Stokes equations in the whole plane with a compactly supported force term and with a prescribed constant limit of a solution at spatial infinity. It is proved that if the force is small enough, then the solution to this problem is unique in the class of all $D$-solutions. We prove also, that the Leray “invading domain method” is always applicable to a given problem in the general case. Furthermore, the Leray solution has a prescribed limit at infinity if the force is small enough. The main tools here are two new general estimates of the difference between mean values of the velocity over two concentric circles in terms of the Dirichlet integral between these two circles, which are also of independent interest.