On the stationary solutions
of the Navier–Stokes equations
in the plane


Julien Guillod
Princeton University
October 6, 2016
1. Introduction
Description of the problem
- Exterior domain $$\Omega=\mathbb{R}^2\setminus\overline{B} \quad\text{with}\quad B \quad\text{bounded}$$
- Stationary Navier–Stokes equations $$\Delta\bu-\bnabla p=\bu\bcdot\bnabla\bu \qquad \bnabla\bcdot\bu=\bzero$$
- Boundary conditions $$\bu|_{\partial B}=\bu^* \quad\text{and}\quad \lim_{|\bx|\to\infty}\bu = \bu_\infty$$
Topological method
Leray–Schauder fixed point
- Construction of weak solutions
by Jean Leray in 1933 - Method of invading domains
- Resolution in the bounded domains $$\Omega_k = \Omega\cap B(\bzero,k)$$
- Weak convergence of the sequence $(\bu_k)_{k\in\mathbb{N}}$ to some $\bu$ with $\bnabla\bu\in L^2(\Omega)$
Perturbation method
Banach fixed point
- Linearization around $\bu=\bu_\infty$ $$\Delta\bu-\bnabla p-\bu_\infty\bcdot\bnabla\bu=\bff \qquad \bnabla\bcdot\bu=\bzero \qquad \lim_{|\bx|\to\infty}\bu=\bzero$$
- Oseen equations if $\bu_\infty\neq\bzero$ : well-posed system
existence of solutions for small data through a fixed point argument (Finn, 1965; Finn & Smith, 1967)
- Stokes equations if $\bu_\infty=\bzero$ : ill-posed system
a priori no solutions even for small data (Stokes paradox, 1856)
- In the talk: $\bu_\infty=\bzero$ for small data
2. Navier–Stokes equations
with $\bu_\infty=\bzero$
Scaling symmetry
- Scaling symmetry of the Navier–Stokes equations in $\mathbb{R}^n$ $$\bu(\bx) \mapsto \bu_\lambda(\bx) = \e^{\lambda}\bu(\e^{\lambda}\bx) \quad \text{for all} \quad \lambda\in\mathbb{R}$$
- A Banach space $X$ is scale-invariant if $${\Vert\bu_\lambda\Vert}_X = {\Vert\bu\Vert}_X$$
- Examples of scale-invariant spaces $X$ $$\begin{gathered}L^{n}(\mathbb{R}^{n})\\L^{n,\infty}(\mathbb{R}^{n})\end{gathered} \qquad\begin{gathered}\dot{H}^{n/2-1}(\mathbb{R}^{n})\\BMO^{-1}(\mathbb{R}^{n})\end{gathered} \qquad\begin{gathered}B_{p,q}^{-1+n/p}(\mathbb{R}^{n})\\X_{1}(\mathbb{R}^{n})\end{gathered}$$ where $$X_\alpha(\mathbb{R}^n) = \big\{\bu:\sup_{\bx\in\mathbb{R}^{n}}\vert\bx\vert^\alpha\vert\bu\vert<\infty\big\}$$
- Main characterization$$\vert\bx\vert^{-1} \in X \text{ or nearly}$$
Criticality
for the time-dependant problem
- Power counting near $\vert\bx\vert=0$ $$\begin{align} \bu & \sim\left|\bx\right|^{-\alpha} & \bnabla\bu & \sim\left|\bx\right|^{-\alpha-1}\\ \Delta\bu & \sim\left|\bx\right|^{-\alpha-2} & \bu\bcdot\bnabla\bu & \sim\left|\bx\right|^{-2\alpha-1} \end{align}$$
-
Subcritical:linearity dominates $\quad\Longleftrightarrow\quad \color{green}{\alpha<1}$
-
Critical:$-\alpha-2 = -2\alpha-1 \quad\Longleftrightarrow\quad \color{yellow}{\alpha=1}$
-
Supercritical:nonlinearity dominates $\quad\Longleftrightarrow\quad \color{red}{\alpha>1}$
Criticality
for the steady-state problem
- Power counting near $\vert\bx\vert=\infty$ $$\begin{align} \bu & \sim\left|\bx\right|^{-\alpha} & \bnabla\bu & \sim\left|\bx\right|^{-\alpha-1}\\ \Delta\bu & \sim\left|\bx\right|^{-\alpha-2} & \bu\bcdot\bnabla\bu & \sim\left|\bx\right|^{-2\alpha-1} \end{align}$$
-
Subcritical:linearity dominates $\quad\Longleftrightarrow\quad \color{green}{\alpha>1}$
-
Critical:$-\alpha-2 = -2\alpha-1 \quad\Longleftrightarrow\quad \color{yellow}{\alpha=1}$
-
Supercritical:nonlinearity dominates $\quad\Longleftrightarrow\quad \color{red}{\alpha<1}$
Net force
- Navier–Stokes equations $$\bnabla\bcdot\mathbf{T}=\bzero$$ where $\mathbf{T}$ is the stress tensor $$\mathbf{T}=\bnabla\bu+\left(\bnabla\bu\right)^{T}-p\,\boldsymbol{1}-\bu\otimes\bu$$
- Invariant quantity $$\int_{\partial B} \mathbf{T}\bcdot\bn = \int_{\partial B(\bzero,r)} \mathbf{T}\bcdot\bn$$
- Net force $$\bF=\int_{\partial B}\!\mathbf{T}\bcdot\bn=\lim_{r\to\infty}\int_{\partial B(\bzero,r)}\!\!\mathbf{T}\bcdot\bn$$
Net force and criticality
- Power counting $$\mathbf{T}=\bnabla\bu+\left(\bnabla\bu\right)^{T}-p\,\boldsymbol{1}-\bu\otimes\bu \sim \left|\bx\right|^{-\min(\alpha+1,2\alpha)}$$
- Net force in dimension $n$ $$\bF = \lim_{r\to\infty}\int_{\partial B(\bzero,r)}\!\!\mathbf{T}\bcdot\bn = \lim_{r\to\infty}r^{n-1} \int_{S^{n-1}}\!\!\mathbf{T}\bcdot\bn$$
- In two dimensions ($n=2$) $$\bF \neq \bzero \quad\text{and}\quad |\bF|<\infty \quad\Longleftrightarrow\quad \color{red}{\alpha=\frac{1}{2}}$$
- In three dimensions ($n=3$) $$\bF \neq \bzero \quad\text{and}\quad |\bF|<\infty \quad\Longleftrightarrow\quad \color{yellow}{\alpha=1}$$
Consequences
| $n=2$ | $n=3$ | |||||
| $\bF\neq\bzero$ | $\bF=\bzero$ | $\bF\neq\bzero$ | $\bF=\bzero$ | |||
| Decay for $\bF\neq\bzero$ | $\color{red}{|\bx|^{-1/2}}$ | $\color{yellow}{|\bx|^{-1}}$ | ||||
| Stokes solutions | $\color{red}{\log|\bx|}$ | $\!\!\color{yellow}{|\bx|^{-1}}$ | $\color{yellow}{|\bx|^{-1}}$ | $\color{green}{|\bx|^{-2}}$ | ||
| Navier–Stokes solutions | $\color{red}{|\bx|^{-1/3}}$ | $\color{red}{|\bx|^{-1/3}}$ | $\color{yellow}{|\bx|^{-1}}$ | $\color{green}{|\bx|^{-2}}$ | ||
| Asymptotic behavior | single wake | double wake, spirals,...? | Landau solution | Stokes solution | ||
The linear equations dominate at infinity, so the problem is easy by a fixed point argument.
Compatibility conditions corresponding to the net force lifted by the Landau solution (Korolev & Šverák, 2011).
Three compatibility conditions (torque,...) cancelled by symmetries or reduced by an harmonic solution (Guillod, 2015).
Numerical solutions decaying like $|\bx|^{-1/3}$ whish is astonishing in view of the three-dimensional case (Guillod, 2015).
Asymptotic expansion decaying like $|\bx|^{-1/3}$ and validations by numerical simulations (Guillod & Wittwer, 2015a).
3. Asymptotic behavior
when $\bF\neq\bzero$
Dominant term
of the asymptotic expansion
- Net force invariant: homogenous decay like $|\bx|^{-1/2}$
- Euler equations dominate at infinity $$ -\bnabla p - \bu\bcdot\bnabla\bu = \bff$$
- Exact solution with $\,\bff=\bF\delta^2(\bx)$ $$\boldsymbol{U}_\bF=\frac{\bphi_\bF(\hat{\bx})}{|\bx|^{1/2}}$$ where $\bphi_\bF$ is a function depending only on the direction of $\bx$
Idea: wake
- Idea: inhomogeneous decay so new power counting
- Parts of the linearity and of the nonlinearity remain dominant at infinity
- Wake for $p,q>0$ $$u(r,\theta) = \frac{1}{r^q}\varphi(r^p \theta)$$
$$u(r,\theta) \quad\text{for}\quad \varphi(z)=\mathrm{e}^{-z^2}$$

$$r^q u(r,\theta) \quad\text{for}\quad \varphi(z)=\mathrm{e}^{-z^2}$$

Ansatz
- Wake condition (linearity and non-linearity both dominant) $$2p+q=1$$
- Net force finite and nonzero $$p=q=\frac{1}{3}$$
- Ansatz $$\boldsymbol{U}_\bF = \frac{1}{r^{1/3}} \varphi_\bF\left(r^{1/3}\theta\right)\be_r$$
- Remark on the scaling $$\lambda \boldsymbol{U}_\bF(\lambda\bx) = \boldsymbol{U}_{\lambda\bF}(\bx)\quad\text{for all}\quad\lambda>0$$
Dominant term
of the asymptotic expansion
- Ansatz into the Navier–Stokes equations
- A large distances, dominant term given by an ordinary differential equation
- Explicit solution $$\varphi_\bF(z) = -6 a^2 \mathrm{sech}^2\left(a z\right)$$ where $$a=\left(\frac{|\bF|}{48}\right)^{1/3}$$
- Solution of the Navier–Stokes equations with a remainder $O\big(|\bx|^{-6/3}\big)$
- The decay of the remainder can be impoved by calculating the next orders
Behavior of the asymptotic expansion
up to second order
The second order $\boldsymbol{U}_\bF^{(2)}$ is explicit and decays like $|\bx|^{-2/3}$ at infinity
$$|\bx|^{1/3} \left| \boldsymbol{U}_\bF(\bx) + \boldsymbol{U}_\bF^{(2)}(\bx) \right|$$
$$\bu \sim |\bx|^{-1/3}$$
$$\bu \sim |\bx|^{-1}$$

Numerical validation

- Exterior of a disk with $\bu^*=(\lambda,0)$
- Domain truncated by a ball of radius $R=10^5$
- Boundary condition on $\partial B(\bzero,R)$ : $\bu=\bzero$


Conjecture
4. Asymptotic behavior
when $\bF=\bzero$
Solutions of the linearized problem
- Asymptotic expansion of the Stokes solutions: $$\bu = \mathcal{M} \bu_0 + \mathcal{A} \bu_a + \mathcal{B} \bu_b + O\big(\color{green}{|\bx|^{-2}}\big) \quad\text{with}\quad \mathcal{M},\mathcal{A},\mathcal{B}\in\mathbb{R}$$



Dominant term
of the asymptotic expansion
- Critical case with a decay like $|\bx|^{-1}$
- By analogy with the three-dimensional case: scale-invariant solution
- Scale-invariant solutions $$e^\lambda\bu(e^\lambda\bx) = \bu(\bx)\quad\text{for all}\quad \lambda\in\mathbb{R}$$
- The scale-invariant solutions are (Šverák, 2011) $$\bu_0 = \frac{\mu}{r}\be_\theta \quad\quad \text{or} \quad\quad \bu_k = \frac{\varphi_k(\theta-\theta_0)}{r}\be_r$$ for $\mu\in\mathbb{R}$, $\theta_0\in\mathbb{R}$, and $k\in\mathbb{N}$ with $k\geq 2$
Dominant term
second attempt
- Idea: enlarge the symmetry group corresponding to the scale-invariant solutions.
- Generalized scale-invariant solutions: $$e^\lambda\bu(e^\lambda\bx) = \mathbf{R}^{-1}_{\eta\lambda}\bu(\mathbf{R}_{\eta\lambda}\bx)$$


Existence and uniqueness
of generalized scale-invariant solutions
Generalized scale-invariant solutions
for $\eta=\,$ 0.0

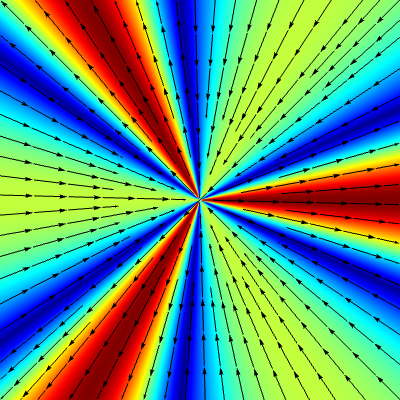
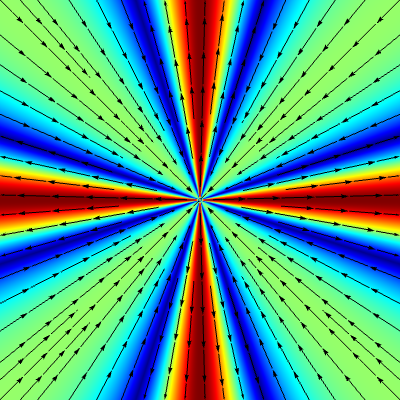
Small solutions
and asymptotic behavior
- Only two small solutions $$k=0 \;\;\&\;\; |\mu|\ll 1 \quad\quad\text{and}\quad\quad k=2 \;\;\&\;\; \theta_0\in\mathbb{R} \;\;\&\;\; |\eta|\ll 1$$
- Three parameters but only two solutions (no superposition)
Numerical simulations
for $\boldsymbol{\mathcal{M}}=\,$ 0.0$\pi$ and $\boldsymbol{\mathcal{A}}=\,$ 0.0$\pi$



5. Conclusions
Conclusions
- Formal arguments and numerical simulations indicate the existence of stationary solutions to the Navier–Stokes equations with a zero velocity at infinity.
- Conjectures on the asymptotic behaviors with a velocity field decaying like $|\bx|^{-1/3}$.
- Linearization around the asymptote: supercritical perturbation of the Stokes equations, so difficult problem.
- Interplay between the linearity and the nonlinearity might be crucial in other open problems.
References
Guillod J. & Wittwer P. 2015a
Asymptotic behaviour of solutions to the stationary Navier–Stokes equations in two-dimensional exterior domains with zero velocity at infinity.
Math. Mod. Meth. Appl. S.Guillod J. & Wittwer P. 2015b
Generalized scale-invariant solutions to the two-dimensional stationary Navier–Stokes equations. SIAM J. Math. Anal.Guillod J. 2015
Steady solutions of the Navier–Stokes equations in the plane.
arXiv:1511.03938