Stationary Navier–Stokes equations
in two dimensions

Julien Guillod
Université Paris Diderot
9 juin 2017

Description of the problem
- Stationary incompressible Navier–Stokes equations $$-\Delta\bu+\bnabla p + \bu\bcdot\bnabla\bu = \bff \qquad \bnabla\bcdot\bu=0$$ in $\mathbb{R}^n$ with $n=2,3$ and for a given forcing term $\bff$
- Boundary condition at infinity $$\lim_{|\bx|\to\infty}\bu=\bu_\infty$$ for a given $\bu_\infty\in\mathbb{R}^n$
Fundamental properties
- a priori bound on the enstrophy
↳ topological methods - invariance by a scaling symmetry
↳ perturbative methods
Topological methods
A priori bound on the enstrophy
$$\int_{\mathbb{R}^n} \bnabla\bu:\bnabla\bu + \underbrace{\int_{\mathbb{R}^n} (\bu\bcdot\bnabla\bu)\bcdot\bu}_{=\,0} = \int_{\mathbb{R}^n} \bff\bcdot\bu$$ $$\implies \Vert\bnabla\bu\Vert_{L^2}^2 = \langle\bff,\bu\rangle_{L^2}$$
Formal a priori bound
If $\bff$ satisfies $$|\langle\bff,\bu\rangle_{L^2}| \leq C \Vert\bnabla\bu\Vert_{L^2}$$
for some $C>0$, then
$$\Vert\bnabla\bu\Vert_{L^2} \leq C$$
Weak solutions
Natural space
$$\dot{H}^1_{\sigma} = \bigl\{\bu \in \dot{H}^1: \bnabla\bcdot\bu=0 \bigr\}$$
Definition (weak solutions)
A vector field $\bu∶\mathbb{R}^n\to\mathbb{R}^n$ is called a weak solution if
- $\bu\in\dot{H}^1_{\sigma}$
- $$\bigl\langle\bnabla\bu,\bnabla\bphi\bigr\rangle_{L^{2}}+\bigl\langle\bu\bcdot\bnabla\bu,\bphi\bigr\rangle_{L^{2}}=\bigl\langle\bff,\bphi\bigr\rangle_{L^{2}}$$
$$\forall\bphi\in C^\infty_{0,\sigma}=\bigl\{\bphi\in C^{\infty}_0: \bnabla\bcdot\bphi=0 \bigr\}$$
Existence of weak solutions in $\mathbb{R}^3$
Theorem (Leray, 1933)
If there exists $C>0$ such that
$$|\langle\bff,\bphi\rangle_{L^2}| \leq C \Vert\bnabla\bphi\Vert_{L^2} \quad \forall \bphi\in C^\infty_{0,\sigma}$$
then for any $\bu_\infty\in\mathbb{R}^3$ there exists a weak solution $\bu$ in $\mathbb{R}^3$ such that
$$\int_{S^2}|\bu-\bu_\infty|^2 = O\left(\frac{1}{|\bx|}\right).$$
Remark
Similar result in three-dimensional exterior domains with Lipshitz boundary.
Existence of weak solutions in $\mathbb{R}^2$
Theorem (Guillod & Wittwer, 2017)
If there exists $C>0$ such that
$$|\langle\bff,\bphi\rangle_{L^2}| \leq C \Vert\bnabla\bphi\Vert_{L^2} \quad \forall \bphi\in C^\infty_{0,\sigma}$$
then for any $\bmu\in\mathbb{R}^2$ there exists a weak solution $\bu$ in $\mathbb{R}^2$ such that
$$\textstyle\int_{B_1}\bu=\bmu.$$
Remark
In two-dimensional exterior domains $\Omega\neq\mathbb{R}^2$, the existence of weak solutions was obtained by Leray (1933).
In this case the parameterization of the weak solution by some $\bmu\in\mathbb{R}^2$ is open.
Strategy of proof
Method of exhaustion
- Find a large enough Hilbert subspace $\mathcal{H}\subset\dot{H}^1_\sigma$ such that $$\mathcal{H}\subset H^1_{\mathrm{loc}} \Subset L^4_{\mathrm{loc}}$$ ↳ Hardy inequality
- Construct a weak solution $\bu_k=\bu_{\infty,1} + \bv_k$ in the ball $B_k$ such that
the sequence $(v_k)_{k\geq1}$ is uniformly bounded in $\mathcal{H}$
↳ a priori bound in bounded domains
↳ compactness of the nonlinearity in bounded domains
↳ Leray–Schauder fixed point theorem - Pass to the limit in the weak formulation
↳ local compactness property of $\mathcal{H}$
Step 1: Hardy inequality in $\mathbb{R}^3$
Hardy inequality (Hardy, 1934)
For any $\bu\in \dot{H}^1_\sigma$, there exists a unique $\bu_\infty\in\mathbb{R}^3$ such that
$$\left\Vert \frac{\bu-\bu_\infty}{|\bx|} \right\Vert_{L^2} \leq 2 \Vert \bnabla\bu \Vert_{L^2}$$
and moreover $\bu-\bu_\infty\in L^6$ and
$$\int_{S^2}|\bu-\bu_\infty|^2 = O\left(\frac{1}{|\bx|}\right).$$
Hilbert subspace
The following subspace of $\dot{H}^1_\sigma$ has a nondegenerate norm:
$$\mathcal{H} = \bigl\{\bu\in\dot{H}^1_\sigma : \bu_\infty=\bzero\bigr\}
= \dot{H}^1_\sigma \cap L^6
\subset H^1_{\mathrm{loc}} \Subset L^4_{\mathrm{loc}}$$
Step 1: Hardy inequality in $\mathbb{R}^2$
Hardy inequality (Guillod & Wittwer, 2017)
There exists a constant $C>$ such that for any $\bu\in \dot{H}^1_\sigma$,
$$\left\Vert \frac{\bu-\bmu}{\langle\bx\rangle\langle\log\langle\bx\rangle\rangle} \right\Vert_{L^2} \leq C \Vert \bnabla\bu \Vert_{L^2}$$
where $\bmu\in\mathbb{R}^2$ is the mean of $\bu$ on the ball of radius one
$$\bmu = \frac{1}{|B_1|}\int_{B_1} \bu.$$
Hilbert subspace
The following subspace of $\dot{H}^1_\sigma$ has a nondegenerate norm:
$$\mathcal{H} = \bigl\{\bu\in\dot{H}^1_\sigma : \bmu=\bzero\bigr\}
\subset H^1_{\mathrm{loc}} \Subset L^4_{\mathrm{loc}}$$
Remark on the hypothesis on $\bff$
Corollary in $\mathbb{R}^3$
In $\mathbb{R}^3$ if $|\bx|\;\bff \in L^2$, then there exists $C>0$ such that
$$|\langle\bff,\bphi\rangle_{L^2}| \leq C \Vert\bnabla\bphi\Vert_{L^2} \quad \forall \bphi\in C^\infty_{0,\sigma}$$
Corollary in $\mathbb{R}^2$
In $\mathbb{R}^2$ if $\langle\bx\rangle\langle\log\langle\bx\rangle\rangle\;\bff \in L^2$ and
$$\int_{\mathbb{R}^2}\bff=\bzero$$
then there exists $C>0$ such that
$$|\langle\bff,\bphi\rangle_{L^2}| \leq C \Vert\bnabla\bphi\Vert_{L^2} \quad \forall \bphi\in C^\infty_{0,\sigma}$$
Step 2: weak solution in $B_k$
- search the solution as $\bu_k=\bu_{\infty,1} + \bv_k$ with $\bv_k \in \mathcal{H}$
- choice of boundary condition $$\bv_k|_{\partial B_k}=\bc_k$$ where $\bc_k=\bzero$ for $n=3$ and $\bc_k\in\mathbb{R}^2$ is used to ensure that $\int_{B_1}\bv_k=\bzero$ when $n=2$
- define $\bw_k=\bv_k-\bc_k$ so that $\bw_k\in\dot{H}^1_{0,\sigma}=\dot{H}^1_\sigma \cap \dot{H}^1_0$
- rewrite the weak formulation as $\bw_k=T\bw_k$ on $\dot{H}^1_{0,\sigma}$
- $T$ is compact since $\dot{H}^1_0 \subset H^1 \Subset L^4$ in bounded domains
- a priori bound on the solutions of $\bw_k=\lambda T\bw_k$ for $\lambda\in[0,1]$ $$\Vert\bnabla\bw_k\Vert_{L^2}^2 \leq \lambda|\langle\bff,\bw_k\rangle_{L^2}| \leq C \Vert\bnabla\bw_k\Vert_{L^2}$$
- apply the fixed point theorem of Leray–Schauder
Step 3: passing to the limit
- since $(\bv_k)_{k\geq1}$is uniformly bounded in $\mathcal{H}$, there exists a subsequence converging to $\bv$ weakly in $\mathcal{H}$ and strongly in $L^4_{\mathrm{loc}}$
- let $\bphi\in C^{\infty}_{0,\sigma}$ and $m$ such that $\mathrm{supp}(\bphi)\subset B_m$
- since $\bu_k = \bu_{\infty,1} + \bv_k$ is a weak solution in $B_k$, for any $k\geq m$ $$\bigl\langle\bnabla\bv_{k},\bnabla\bphi\bigr\rangle_{L^{2}} + \bigl\langle(\bu_{\infty,1}+\bv_{k})\bcdot\bnabla\bv_{k},\bphi\bigr\rangle_{L^{2}} = \bigl\langle\bff,\bphi\bigr\rangle_{L^{2}}$$
- in the limit $k\to\infty$ $$\bigl\langle\bnabla\bv,\bnabla\bphi\bigr\rangle_{L^{2}} + \bigl\langle(\bu_{\infty,1}+\bv)\bcdot\bnabla\bv,\bphi\bigr\rangle_{L^{2}} = \bigl\langle\bff,\bphi\bigr\rangle_{L^{2}}$$ so $\bu = \bu_\infty + \bv$ is a weak solution in $\mathbb{R}^3$
- moreover, by weak convergence $$\Vert\bnabla\bu\Vert_{L^2} = \Vert\bnabla\bv\Vert_{L^2} \leq \liminf_{k\to\infty}\Vert\bnabla\bv_k\Vert_{L^2}\leq C$$
Limit at infinity in $\mathbb{R}^2$
Theorem (Gilbarg & Weinberger, 1978)
If $\bu$ is a weak solution in $\mathbb{R}^2$, then either there exists $\bu_0\in\mathbb{R^2}$ such that
$$\lim_{\left|\bx\right|\to\infty}\int_{S^{1}}\left|\bu-\bu_{0}\right|^{2}=0$$
or
$$\lim_{\left|\bx\right|\to\infty}\int_{S^{1}}\left|\bu\right|^{2}=\infty$$
Consequence
The limit at infinity of the weak solutions
is widely open in two dimensions.
is widely open in two dimensions.
Perturbative methods
Scaling symmetry
Scaling symmetry
$$\begin{align}
\bu(\bx) &\mapsto \bu_\lambda(\bx) = \lambda \bu(\lambda\bx)\\
p(\bx) &\mapsto p_\lambda(\bx) = \lambda^2 p(\lambda\bx)\\
\bff(\bx) &\mapsto \bff_\lambda(\bx) = \lambda^3 \bff(\lambda\bx)\\
\end{align}$$
Remark
The scaling symmetry describes the link
between the linearity and the nonlinearity.
between the linearity and the nonlinearity.
Criticality
Criticality
- subcritical space
↳ linearity dominant - critical space
↳ linearity and nonlinearity balanced - supercritical space
↳ nonlinearity dominant
Criticality of a Banach space $X$
$$\Vert \bu_\lambda \Vert_X = \lambda^{1-\alpha} \Vert\bu\Vert_X$$
- $\alpha<1$ : subcritical locally and supercritical at infinity
- $\alpha=1$ : critical both locally and at infinity
- $\alpha>1$ : supercritical locally and subcritical at infinity
Examples of function spaces
Function space for weak solutions
$\dot{H}^1_\sigma$ has $\alpha=\frac{n}{2}-1$, so for $n=2,3$ it is
- subcritical locally (linearity locally dominant)
↳ no regularity problem - supercritical at infinity (nonlinearity dominant at infinity)
↳ a priori no boostrap from weak solutions
Function space for perturbative solutions
$$E_\alpha = \bigl\{ \bu\in L^1_{\mathrm{loc}}: {\textstyle\sup_{\bx\in\mathbb R^n}} (1+|\bx|^{\alpha}) |\bu(\bx)| <\infty \bigr\}$$
is subcritical locally and
- subcritical at infinity if $\alpha>1$
- supercritical at infinity if $\alpha<1$
Perturbation method
when $\bu_\infty\neq\bzero$
Linearization around $\bu_\infty\neq\bzero$ (Oseen equations)
$$-\Delta\bu+\bnabla p + \bu_\infty\bcdot\bnabla\bu = \bff \qquad \bnabla\bcdot\bu=0$$
Theorem (Finn, 1965; Babenko, 1973; Galdi, 1992)
If $\bu$ is a weak solution in $\mathbb{R}^3$ with $\bu_\infty\neq\bzero$, then
$\bu$ behaves at infinity like the Oseen fundamental solution.
Theorem (Finn & Smith, 1967; Galdi, 1992)
Let $q\in(1,6/5]$ and $\bu_\infty\neq\bzero$. If $\bff\in L^q$ is small enough, then there exists a solution $\bu$
behaving at infinity like the Oseen fundamental solution.
Net force and decay
when $\bu_\infty=\bzero$
- Navier–Stokes equivalent to $\bnabla\bcdot\mathbf{T}=\bff$ where $$\mathbf{T}=\bnabla\bu+\left(\bnabla\bu\right)^{T}-p\,\boldsymbol{1}-\bu\otimes\bu$$
- Invariant quantity $$\int_{B_r}\bff = \int_{\partial B_r}\!\mathbf{T}\bcdot n$$
- Net force $$\bF = \int_{\mathbb{R}^n}\bff = \lim_{r\to\infty}\int_{\partial B_r}\!\mathbf{T}\bcdot\bn = \lim_{|\bx|\to\infty}|\bx|^{n-1}\int_{S^{n-1}}\!\mathbf{T}\bcdot\bn$$
Consequence
If $\bu\in E_\alpha$ with $\alpha>\frac{n-1}{2}$, then $\bF=\bzero$.
Perturbative solutions in $\mathbb{R}^3$
when $\bu_\infty=\bzero$
Landau solution
For $\bF\in\mathbb{R}^3$, the Landau solution $\bU_\bF$ is a scale-invariant solution of the Navier–Stokes equations with
$\bff = \bF \delta(\bx)$.
Theorem (Korolev & Šverák, 2011)
Let $\varepsilon\in(0,1)$. If $\bff\in E_{3+\varepsilon}$ is small enough, then there exists a unique solution $\bu\in E_1$ such that
$$\bu = \bU_\bF + O\Biggl(\frac{1}{|\bx|^{1+\varepsilon}}\Biggr)$$
where $\bF = \int_{\mathbb{R}^3}\bff$. Moreover this solution is unique the among weak solutions having $\bu_\infty=\bzero$.
Perturbative solutions in $\mathbb{R}^2$
when $\bu_\infty=\bzero$
Theorem (Guillod, 2015c; Guillod & Wittwer, 2017)
Let $\varepsilon\in(0,1)$. If $\bff\in E_{3+\varepsilon}$ is small enough with $\bF=\bzero$
and belongs to a manifold of codimension two,
then there exists a unique solution $\bu\in E_1$ such that
$$\bu = -\frac{M}{4\pi}\frac{\bx^\perp}{|\bx|^2} + O\Biggl(\frac{1}{|\bx|^{1+\varepsilon}}\Biggr)$$
where $M = \int_{\mathbb{R}^2}\bx\bwedge\bff$ is the net torque. If $\bff$ is not in this
manifold of codimension two, then the
perturbation method fails in $E_1$.
Moreover, if $M=0$, this solution is unique among the weak solutions having the same $\bmu=\int_{B_1} \bu$.
Moreover, if $M=0$, this solution is unique among the weak solutions having the same $\bmu=\int_{B_1} \bu$.
Conjectures on the
existence of solutions
in $\mathbb{R}^2$ with $\bu_\infty=\bzero$
Open problems
Open problems when $\bF\neq\bzero$
- existence of weak solutions
- existence of perturbative solutions with $\bu_\infty=\bzero$
Open problems when $\bF=\bzero$
- existence of weak solutions with $\bu_\infty=\bzero$
- existence of perturbative solutions if $\bff$ do not satisfies the two compatibility conditions
Question
What is happening without any compatibility conditions on $\bff$, even under smallness assumptions on $\bff$?
Asymptotic expansion when $\bF\neq\bzero$
Theorem (Guillod & Wittwer, 2015a)
For any $\bF\neq\bzero$, there exists a solution
$\bU_\bF\in E_{1/3}$ with some $\bff\in E_{7/3}$ having net force $\bF$.
$$\bU_\bF \sim |\bx|^{-1/3}$$
$$\bU_\bF \sim |\bx|^{-2/3}$$

Numerical simulations when $\bF\neq\bzero$
- Take some $\bff$ having compact support and $\bF\neq\bzero$
- Truncate the domain to a ball of radius $r=10^5$
- Add zero boundary condition on $\partial B_r$: $\bu|_{\partial B_r}=\bzero$
$|\bx|^{1/3}\,|\bu|$

$|\bx|\,|\bu-\bU_\bF|$

Conjecture when $\bF\neq\bzero$
Conjecture (Guillod & Wittwer, 2015a)
For a large class of small $\bff$ with $\bF\neq\bzero$,
there exists a solutions to the Navier–Stokes equations such that
$$\bu = \bU_\bF + O\Biggl(\frac{1}{|\bx|}\Biggr).$$
Main problem
How to invert the linear system
$$-\Delta\bu+\bnabla p+\bU_\bF\bcdot\bnabla\bu+\bu\bcdot\bnabla\bU_\bF=\bff \qquad \bnabla\bcdot\bu=\bzero$$
since $\bU_\bF$ decays only like $|\bx|^{-1/3}$?
Generalized scale-invariant solutions
Definition
Combination of the scaling and rotational symmetries leads to the concept of scale-invariant solutions up to a rotation:
$$e^\lambda\bu(e^\lambda\bx) = \mathbf{R}^{-1}_{\eta\lambda}\bu(\mathbf{R}_{\eta\lambda}\bx)$$
i.e.
$$\bu(r,\theta) = \frac{\bphi(\theta + \eta \log r)}{r}$$


Existence and uniqueness
of scale-invariant solutions up to a rotation
Theorem (Guillod & Wittwer, 2015b)
For $\eta\in\mathbb{R}$ and $k\in\mathbb{N}^*$ satisfying $$\frac{4}{1+\eta^2}\leq k^2,$$
there exists a unique scale-invariant solution up to a rotation of the Navier–Stokes equations in
$\mathbb{R}^2\setminus\{\bzero\}$ which is $k$-fold symmetric.
Generalized scale-invariant solutions
for $\eta=\,$ 0.0
$k=2$


$k=3$
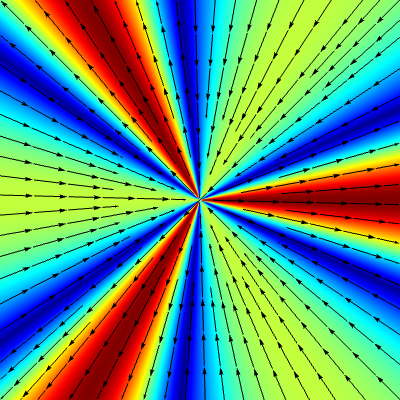

$k=4$
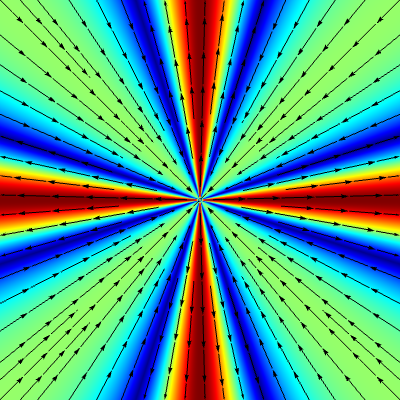

Numerical simulations when $\bF=\bzero$
for $M=\,$ 0.0$\pi$ and $A=\,$ 0.0$\pi$


$A$
$M$
$\bu\sim|\bx|^-$0.00

$|\bx|$0.00$\quad\;|\bu|$
Summary
| $n=2$ | $n=3$ | |||||
| $\bF\neq\bzero$ | $\bF=\bzero$ | $\bF\neq\bzero$ | $\bF=\bzero$ | |||
| Stokes solutions | $\log|\bx|$ | $|\bx|^{-1}$ | $|\bx|^{-1}$ | $|\bx|^{-2}$ | ||
| Navier–Stokes solutions | $\color{red}{|\bx|^{-1/3}}$ | $\color{red}{|\bx|^{-1/3}}$ | $\color{yellow}{|\bx|^{-1}}$ | $\color{yellow}{|\bx|^{-2}}$ | ||
| Asymptotic behavior | single wake? | double wake, spirals,...? | Landau solution | Stokes solution | ||
Conclusion
In $\mathbb{R}^2$ the nonlinearity seems to “help” for the existence!